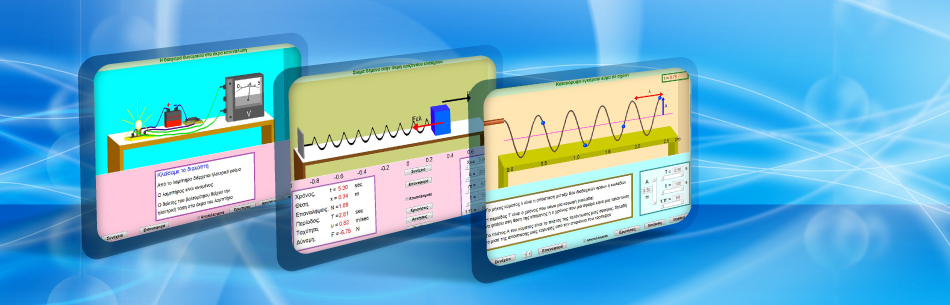
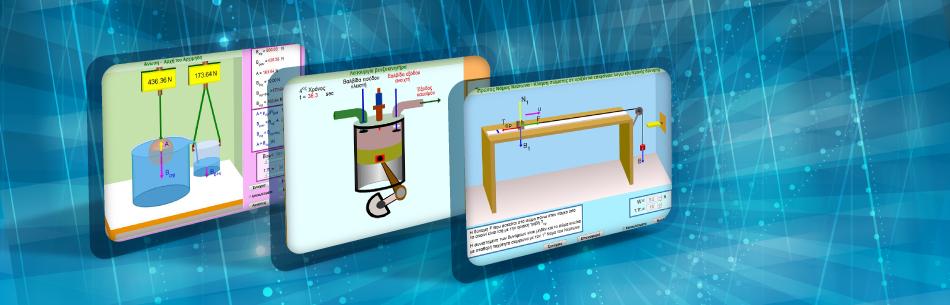
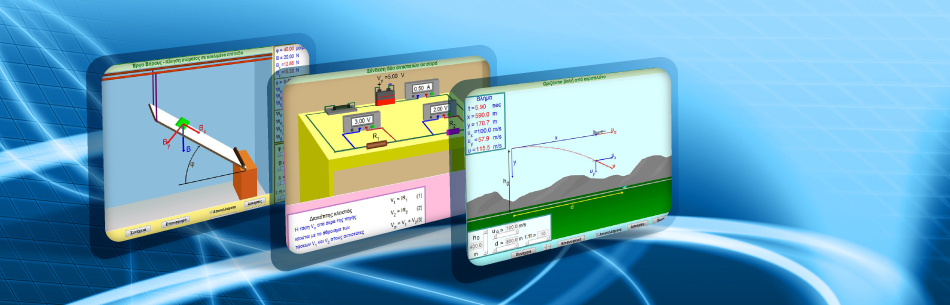
ΠΑΡΟΥΣΙΑΣΕΙΣ ΠΕΙΡΑΜΑΤΩΝ

Α' Λυκείου
>> Δείτε όλα τα Video της Α' Λυκείου

Βαρύτητα

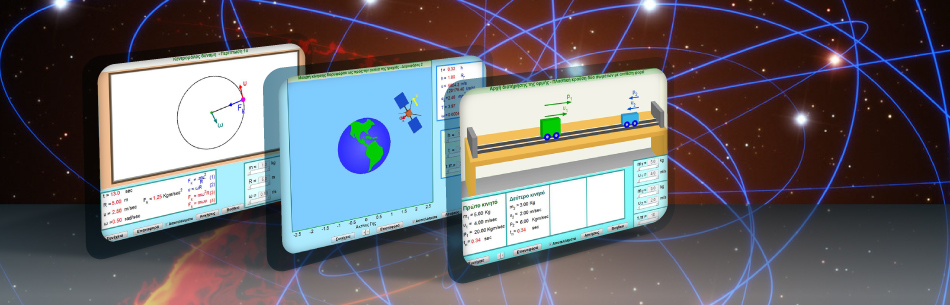
Η κίνηση των δορυφόρων

Μελέτη της κίνησης ως προς την περίοδο - Δορυφόρος 2
1.  Η προσομοίωση δείχνει την κίνηση δορυφόρου.
 
2. Σκοπός της προσομοίωσης είναι η μελέτη της κίνησης δορυφόρου.
 
Ένα κινητό εκτελεί κυκλική κίνηση αν η τροχιά του είναι περιφέρεια κύκλου.
 
Ένα κινητό εκτελεί ομαλή κυκλική κίνηση αν η τροχιά του είναι περιφέρεια κύκλου και η ταχύτητά του έχει σταθερή τιμή.
 
Ο χρόνος που χρειάζεται το κινητό για να κάνει μια περιφορά  λέγεται περίοδος, συμβολίζεται με Τ και έχει μονάδα το δευτερόλεπτο (sec).
 
Η κεντρομόλος δύναμη ενός κινητού που εκτελεί ομαλή κυκλική κίνηση είναι διανυσματικό  μέγεθος και συμβολίζεται με Fκ.
 
Το μέτρο της κεντρομόλου δύναμης ενός κινητού μάζας m που εκτελεί ομαλή κυκλική κίνηση σε περιφέρεια κύκλου ακτίνας R με  γραμμική ταχύτητα υ δίνεται από τη σχέση 

F_{k}=frac{mv^{2}}{R}                                          (1)

Μονάδα της κεντρομόλου δύναμης είναι το N.
 
Το διάνυσμα της κεντρομόλου δύναμης βρίσκεται στο επίπεδο της τροχιάς του κινητού.
Το σημείο εφαρμογής της κεντρομόλου δύναμης είναι το κέντρο μάζας του κινητού.
Η κατεύθυνση του είναι προς το κέντρο του κύκλου.
 
Είναι γνωστό ότι για ένα κινητό που εκτελεί ομαλή κυκλική κίνηση, μεταξύ της γραμμικής και περιόδου ισχύει η σχέση
 
v=frac{2pi R}{T}                                         (2)
 
Από τις σχέσεις (1) και (2) αν απαλείψουμε την ακτίνα R προκύπτει
 
  F_{k}=frac{m2pi v}{T}                                   (3)
 
Από τις σχέσεις (1) και (2) αν απαλείψουμε τη γραμμική ταχύτητα προκύπτει
 
  F_{k}=frac{m4pi^{2}R}{T^{2}}                                 (4)
 
Οι σχέσεις (1), (3) και (4) συνδέουν την κεντρομόλο δύναμη ενός κινητού με τη  μάζα του, τη  γραμμική ταχύτητα, την ακτίνα της τροχιάς και την περίοδο.
 
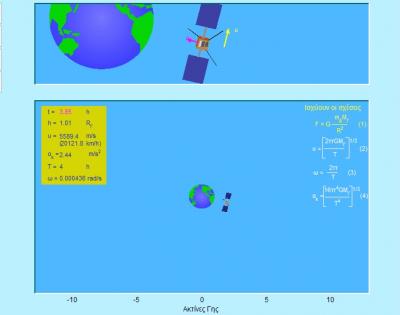
Στην προσομοίωση δείχνεται η κίνηση δορυφόρου γύρο από τη Γη.
 
Όπως αποδεικνύεται η κίνηση αυτή  είναι ομαλή κυκλική κίνηση.
 
Η κεντρομόλος δύναμη , είναι η δύναμη της παγκόσμιας έλξης μεταξύ δύο σωμάτων που δίνεται από τη σχέση

F_{k}=frac{Gm_{1}m_{2}}{R^{2}}                              (5)

όπου m1, m2 είναι οι μάζες τους R η απόστασή τους και G η σταθερά της παγκόσμιας έλξης.
Στην προκειμένη περίπτωση της κίνησης του δορυφόρου γύρο από τη Γη είναι

       F_{k}=frac{GM_{Gamma}m_{Delta}}{R^{2}}                        (6)

όπου mΔ, ΜΓ είναι οι μάζες του δορυφόρου και Γης και  R η απόστασή τους , δηλαδή η απόσταση του δορυφόρου από το κέντρο της Γης.
 
Από τις σχέσεις (1), (2) και (6) αν θέσουμε m = mΔ προκύπτει  η σχέση
 
v=^{3}sqrt{frac{2pi GM_{Gamma}}{Talpha}}                             (7)
 
 
Η κεντρομόλος επιτάχυνση του δορυφόρου δίνεται από τη σχέση

alpha_{k}=frac{v^{2}}{R}                                      (8)

Από τις σχέσεις (2) , (7) και (8) προκύπτει

alpha_{k}=^{3}sqrt{frac{16pi^{4}GM_{Gamma}}{T^{4}}}                      (9)

Τέλος ισχύει η γνωστή σχέση

omega=frac{2pi}{T}                                           (10)

Οι σχέσεις  (7), (9) και (10) δίνουν τις τιμές της γραμμικής ταχύτητας, της κεντρομόλου επιτάχυνσης  και της γωνιακής ταχύτητας  του δορυφόρου σε σχέση με την περίοδό  του γύρο από τη Γη.
 
Το κίτρινο βέλος είναι το διάνυσμα της  γραμμικής ταχύτητας του δορυφόρου.  Το μήκος του είναι ανάλογο της γραμμικής ταχύτητας του δορυφόρου.
 
Το ροζ βέλος είναι το διάνυσμα της  κεντρομόλου επιτάχυνσης  του δορυφόρου.  Το μήκος του είναι ανάλογο της κεντρομόλου επιτάχυνσης  του δορυφόρου.
 
Το διάνυσμα της γωνιακής ταχύτητας εφαρμόζεται στο κέντρο της Γης είναι κάθετο στην τροχιά του δορυφόρου και έχει φορά προς τον παρατηρητή.  Στην προκειμένη περίπτωση δεν δείχνεται.
 
Στο πλαίσιο δείχνεται η τιμή της γραμμικής ταχύτητας, της  κεντρομόλου επιτάχυνσης, του  ύψους και της γωνιακής ταχύτητας του δορυφόρου.
 
Επίσης δείχνεται και η χρονική διάρκεια της κίνησης  σε ώρες.
 
Ο χρήστης του προγράμματος μπορεί να μεταβάλλει την περίοδο του δορυφόρου  και το χρόνο παρατήρησης της κίνησης.
 
Σχόλιο
Αν RΓ είναι η ακτίνα της Γης και h η απόσταση του δορυφόρου από την επιφάνεια της Γης (ύψος δορυφόρου)  τότε η απόσταση Δορυφόρου –Γης είναι
R = RΓ + h
 
3.   Συμπέρασμα από την εκτέλεση της προσομοίωσης
Με την προσομοίωση κατανοείται η κίνηση δορυφόρου.